我实验室曹鑫鑫、孙嘉鑫、顾宇航、秦帆帆、李彦龙、于彦江和宁伏龙教授在Geoenergy Science and Engineering期刊上发表了题为Revised inflow performance relationship for productivity prediction from marine sandy hydrate reservoirs in Nankai Trough的文章。

论文链接：https://doi.org/10.1016/j.geoen.2024.212845

1、文章概述

本文基于南海海槽有限的试采资料和数值拟合数据，提出了两种修正的产能预测方程，对不同降压生产方案下的水合物藏进行流入动态分析，并给出了不同采收率下的IPR曲线。在常规公式的基础上，考虑水合物分解和压降的双重作用，对常规产能方程中的储层压力项进行了修正。对比结果表明，修正后的Vogel方程和Fetkovich方程均能较好地描述单一直井和水平井降压开采的流入动态关系。在此基础上，进一步分析了储层物性参数对IPR曲线的影响，验证了修正IPR方程的适用性。本文旨在对类似砂质水合物储层的安全高效开采提供可行的产能预测方法。

2、研究方法

本文采用数值模拟与拟合回归相结合的手段进行研究。首先，验证日本首次试采的开采产气曲线，在此基础上借助模拟软件进行长时间的开采预测，然后通过拟合和回归分析得到改进的IPR曲线。该方法避免了解析法建立IPR曲线的复杂性，更适用于复杂的多相多组分流动储层。数值模型的开采示意图如图1所示。

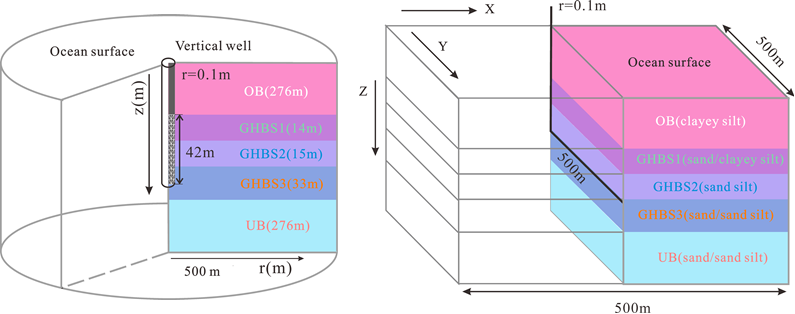
图1 日本砂质水合物储层单一直井和水平井开采示意模型

为了建立适用于特定储层开采的流入动态曲线，首先需要将模拟预测结果归纳为统一的表征形式。随后再对传统的流入动态关系方程进行关键系数修正，使其适用于日本南海海槽天然气水合物储层降压开采，进而提出了修正Vogel方程和Fetkovich方程，方程的具体形式如下：

修正Vogel方程：

；

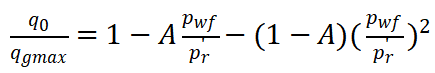修正Fetkovich方程：

；

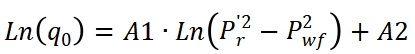其中，pr′为修正后的储层压力(MPa)，该项主要反映降压开采水合物储层时综合供气能力，定义如下：

；

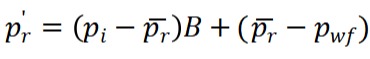其中储层平均压力采用体积加权法计算得到。

3、研究结果

（一）单一直井降压开采水合物储层的流入动态分析

首先，我们对砂质水合物储层在不同采收率下的单一直井开采产气动态进行了分析。预测结果如图2a，随着生产压力的降低，产气速率呈现阶梯上升，在此基础上，我们进行了不同修正IPR方程的拟合程度对比(图2b)，结果表明，修正Vogel方程更加适用于开采这一地区的砂质水合物储层，拟合曲线相关系数高达94.5%。对各种储层物性参数的敏感性分析表明（图2c），孔隙度和水合物饱和度的变化会导致待定系数A的取值不同，这主要是由于直井方式开采时修正Vogel方程中的关键系数修正储层压力项pr′发生了变化。相较之下，绝对渗透率对IPR曲线形状影响甚微。

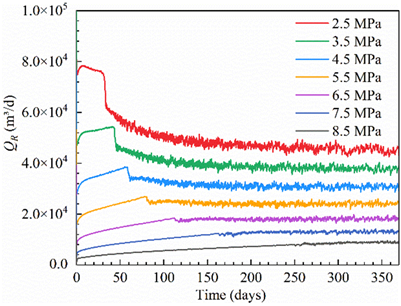
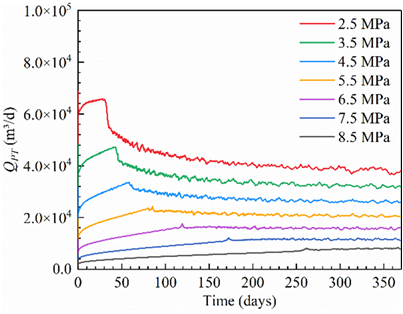
（a）水合物分解产气速率和总产气速率

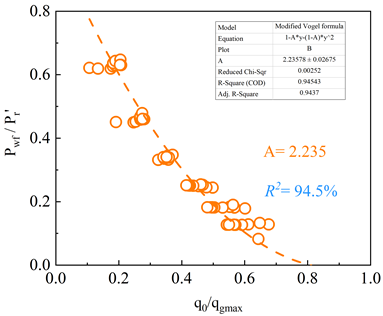
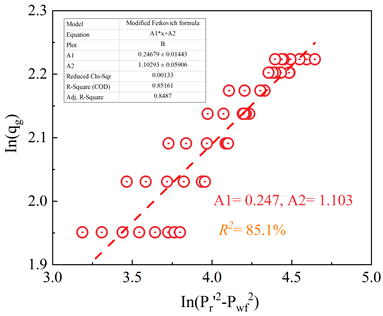
（b）不同修正方程的拟合对比

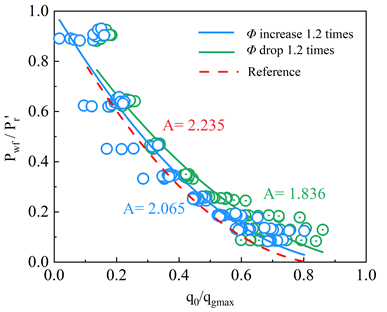
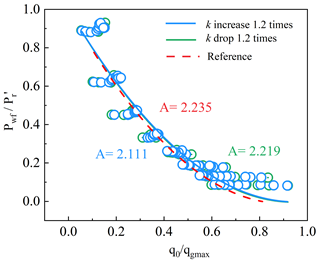
（c）修正IPR曲线的敏感性分析

图2 单一直井降压开采水合物储层的流入动态分析

（二）单一水平井降压开采水合物储层的流入动态分析

类似地，我们也对砂质水合物储层在不同采收率下的单一水平井开采产气动态进行了分析。预测结果如图3a所示，随着生产压力的降低，产气速率峰值速率越早出现，水合物分解驱动力越大。在此基础上，我们进行了不同修正IPR方程的拟合程度对比(图3b)，结果表明，修正Fetkovich方程更加适用于单一水平井开采日本砂质水合物储层，拟合相关系数高达91.7%。对各种储层物性参数的敏感性分析表明（图3c），绝对渗透率对修正IPR曲线的影响至关重要。由于产气量和压力平方差的变化一致，不同孔隙度下的修正IPR曲线呈现出一致的线性趋势。此外，改变水合物饱和度对改进Fetkovich方程影响相对较小。

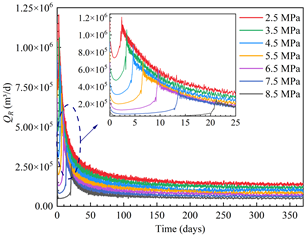
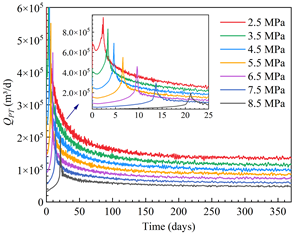
（a）水合物分解产气速率和总产气速率

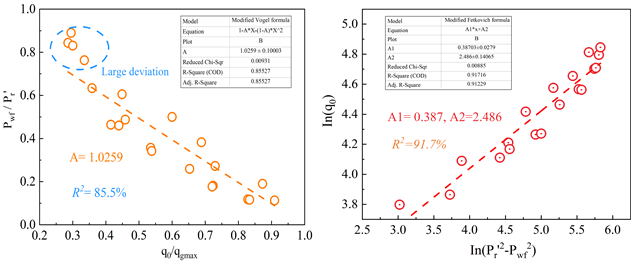
（b）不同修正方程的拟合对比

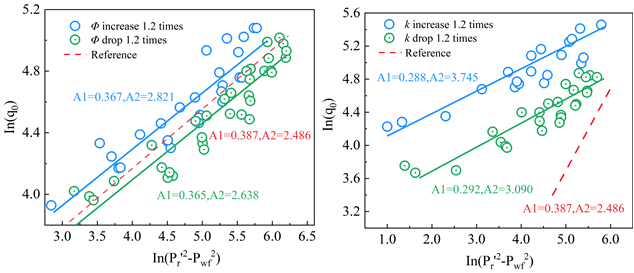
（c）修正IPR曲线的敏感性分析

图3单一水平井降压开采水合物储层的流入动态分析